(엑셀) 회귀분석

 

 

목차

 

 

엑셀을 이용해서 할 수 있는 데이터 분석 방법 중 가장 파워풀한 회귀분석에 대해서 설명드리겠습니다.

​

1. 회귀분석의 정의

 

회귀분석은 아마도 많은 분들께서 들어보셨을 것이고, 실제 업무에서 굉장히 활용도가 높은 데이터 분석 기법 중 하나입니다.

통계학에서, 회귀 분석(回歸 分析, 영어: regression analysis)은 관찰된 연속형 변수들에 대해 두 변수 사이의 모형을 구한뒤 적합도를 측정해 내는 분석 방법이다.

​

회귀분석은 시간에 따라 변화하는 데이터나 어떤 영향, 가설적 실험, 인과 관계의 모델링등의 통계적 예측에 이용될 수 있다. 그러나 많은 경우 가정이 맞는지 아닌지 적절하게 밝혀지지 않은 채로 이용되어 그 결과가 오용되는 경우도 있다. 특히 통계 소프트웨어의 발달로 분석이 용이해져서 결과를 쉽게 얻을 수 있지만 적절한 분석 방법의 선택이였는지 또한 정확한 정보 분석인지 판단하는 것은 연구자에 달려 있다.

https://ko.wikipedia.org/wiki/%ED%9A%8C%EA%B7%80_%EB%B6%84%EC%84%9D

 

회귀분석은 쉽게 말해 연속형인 하나 또는 여러 개의 독립변수(X1, X2, X3, ... , Xn)가 종속변수(Y)에 어떤 관계를 가지는지를 식으로 나타낼 수 있는 방법이라고 보시면 됩니다.

​

ex) Y = aX1 + bX2 + C

​

보통은 어떤 과거 데이터를 이용해 회귀분석한 후 식을 이용해 미래를 예측하는데 활용합니다.

​

2. 사용법과 예시

 

사용법은 예를들어 설명드리도록 하겠습니다.

​

데이터셋은 제일 아래 첨부해놨으니 받아서 해보시기 바랍니다. (임의로 제작한 데이터셋임)

​

아래와 같이 철의 5대 원소인 탄소(C), 규소(Si), 망간(Mn), 인(P), 황(S)과 인장강도 데이터가 있습니다. (과거 상관분석 포스팅 데이터 참조)

​

구하고자 하는 것은 인장강도라는 철강재료의 특성과 다른 성분들의 관계를 식으로 표현해보는 것입니다.

 

지난 포스트를 참고해서 데이터 메뉴의 데이터 분석 기능을 활성화하고 데이터 분석을 선택합니다. 그리고 회귀분석을 선택하고 확인을 눌러주세요.

 

datawithnosense.tistory.com/8

(엑셀) 데이터분석 도구 추가 방법

 

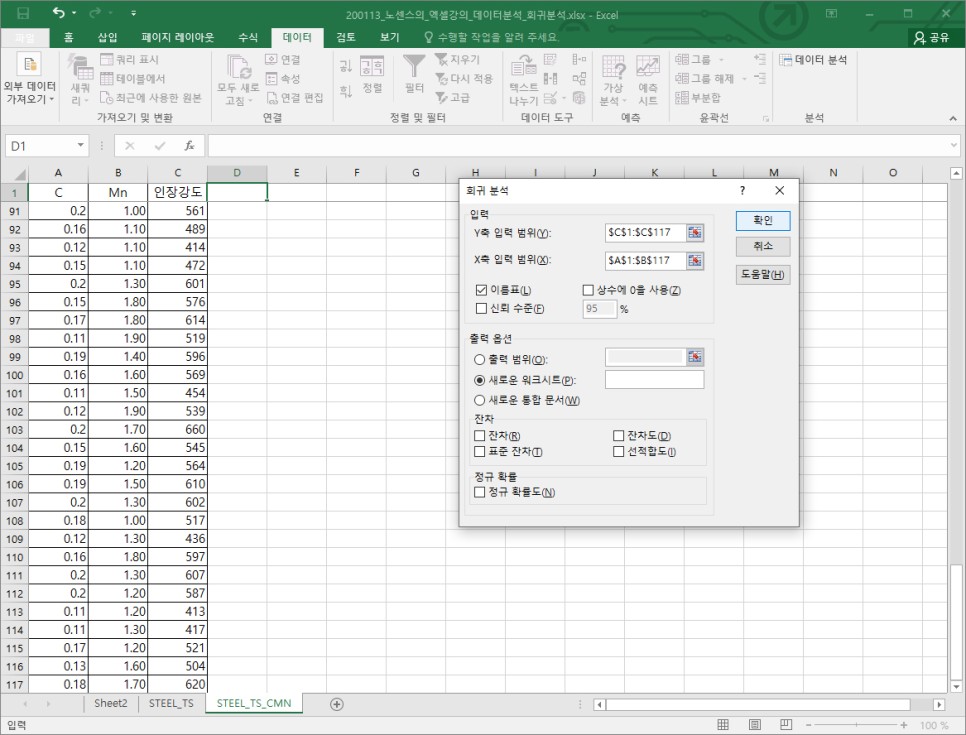
회귀분석 설정화면에서는 『Y축 입력 범위』를 인장강도 열로 선택해주시고, 『X축 입력 범위』는 C, Si, Mn, P, S열 전체를 선택해주세요. 그리고 『이름표』는 체크박스를 선택한(∵ 시트의 첫 행이 데이터가 아니라 열 이름이기 때문에) 후 확인을 선택합니다.

 

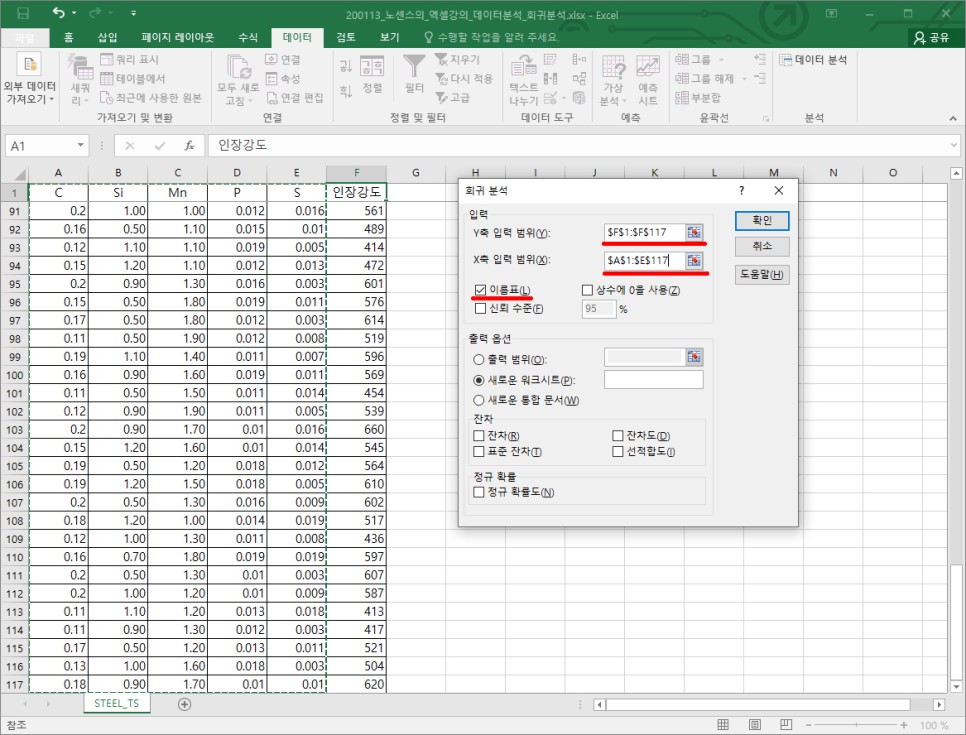
이렇게 되면 아래와 같이 새 워크시트가 하나 열리면서 회귀분석 결과가 출력되게 됩니다.

회귀분석 참 쉽죠?

문제는 여기서 부터입니다.

 

3. 회귀분석 결과 해석

​

회귀분석을 실시하면 결과를 해석할 줄 알아야 올바른 모델을 선택할 수 있습니다. 회귀분석의 결과는 크게 4가지로 구분하여 해석합니다.

① 회귀분석 자체가 통계적으로 유의한가? 유의한 F값이 0.05 보다 낮아야 95% 신뢰수준에서 유의함

② R-Squared(결정계수)가 높은가? 일반적으로 0.7 보다 크면 높은편이라고 하나 상황에 따라 다름

※ R-Squared(결정계수)에 대한 정의는 하기 위키백과 내용 참조

통계학에서, 결정계수(決定係數, 영어: coefficient of determination)는 추정한 선형 모형이 주어진 자료에 적합한 정도를 재는 척도이다. 반응 변수의 변동량 중에서 적용한 모형으로 설명가능한 부분의 비율을 가리킨다. 결정계수의 통상적인 기호는 이다.

일반적으로 모형의 설명력으로 해석되지만 모형에 설명 변수가 들어갈수록 증가하기 때문에 해석에 주의해야 한다. 이러한 문제를 해결하기 위해 조정 결정 계수가 제시되었다.

결정계수의 값은 0에서 1사이에 있으며, 종속변인과 독립변인 사이에 상관관계가 높을수록 1에 가까워진다. 즉, 결정계수가 0에 가까운 값을 가지는 회귀모형은 유용성이 낮은 반면, 결정계수의 값이 클수록 회귀모형의 유용성이 높다고 할 수 있다.

https://ko.wikipedia.org/wiki/%EA%B2%B0%EC%A0%95%EA%B3%84%EC%88%98

 

③ 개별 독립변수의 P값이 통계적으로 유의한가? 개별 P값이 0.05 보다 낮아야 95% 신뢰수준에서 유의함

④ 계수와 절편을 이용해 회귀식을 계산할 수 있음

 

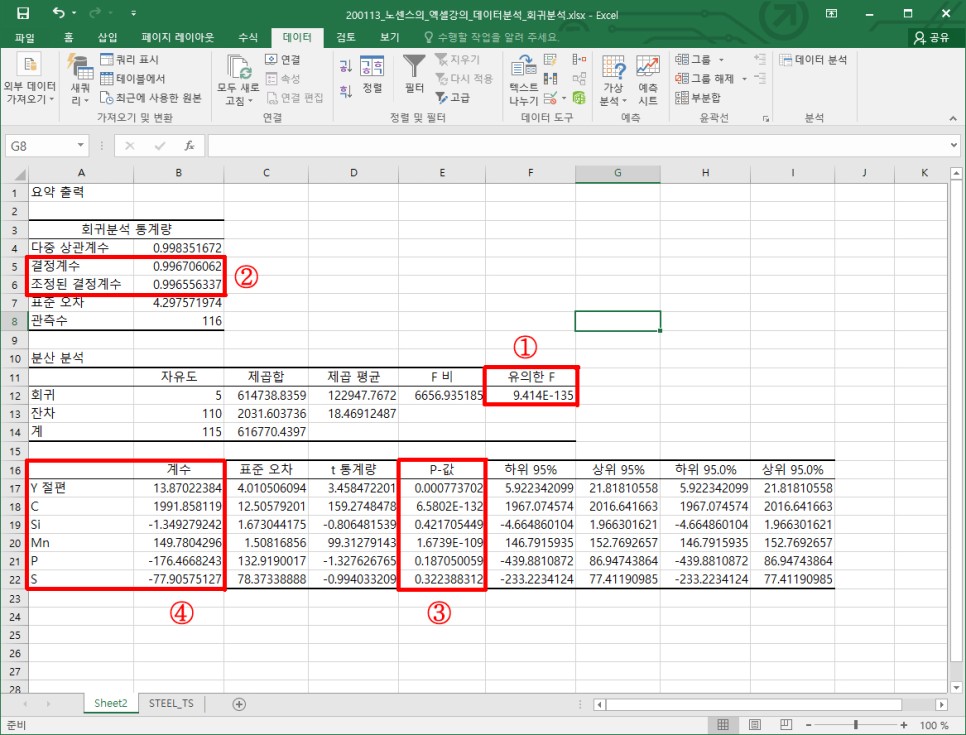
상기와 같은 기준으로 분석결과를 검토하자면

① 회귀분석의 F값이 9.414E-135(=9.414*10^-135 ≒ 0에 가까운 매우 작은 값)으로 0.05 보다 작아 95% 신뢰수준에서 통계적으로 유의하고

② 결정계수와 조정된 결정계수 모두 0.99 이상으로 매우 높고 (최대값은 1)

③ 5개의 독립변수 중 C와 Mn의 p값은 0.05 보다 작아 95% 신뢰수준에서 통계적으로 유의하지만 나머지 변수들은 유의하지 않음

④ Y(인장강도) = 1991.86*C -1.35*Si + 149.78*Mn - 176.47*P - 77.91*S + 13.87 이라는 식으로 표현할 수 있음

​

4. 불필요 변수 제거 후 회귀분석 재실행

 

이번 회귀분석에서는 Si, P, S값이 통계적으로 유의하지 않은 변수들이기 때문에 해당 변수들을 제외하고, 다시 회귀분석을 해보는 게 좋습니다.

​

아래와 같이 데이터가 들어있는 "STEEL_TS" 시트에서 마우스 오른쪽키를 눌러 "이동/복사"를 통해 시트를 복사한 후 다시 회귀분석을 해보겠습니다.

 

복사한 시트이름을 "STEEL_TS_CMN"으로 변경하고 Si, P, S 열을 모두 삭제하여 아래와 같이 C, Mn, 인장강도 데이터만 남게 시트를 수정합니다.

 

이후에는 동일하게 데이터 메뉴의 데이터 분석을 통해 회귀분석을 실시합니다.

 

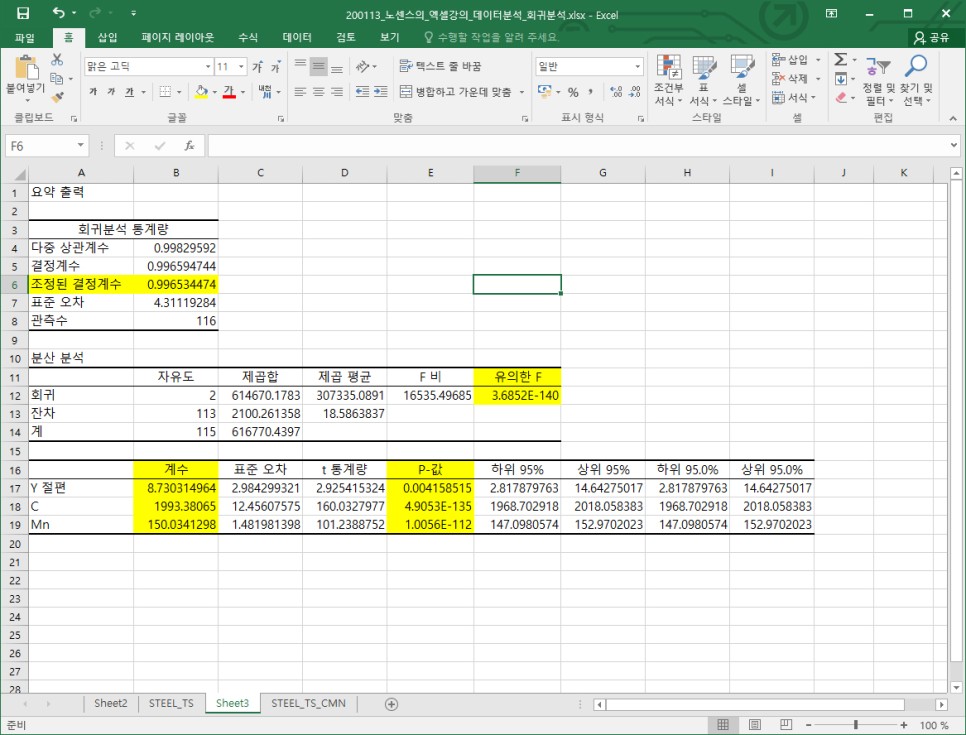
그리고 다시 수행한 회귀분석 결과를 해석해보면

① 회귀분석의 F값이 3.6852E-140(=3.6852*10^-140 ≒ 0에 가까운 매우 작은 값)으로 0.05 보다 작아 95% 신뢰수준에서 통계적으로 매우 유의하고

② 결정계수와 조정된 결정계수 모두 0.99 이상으로 여전히 매우 높고 (최대값은 1)

③ C와 Mn의 p값은 모두 0.05 보다 작아 95% 신뢰수준에서 통계적으로 유의하며

④ Y(인장강도) = 1993.38*C + 150.03*Mn + 8.73 이라는 식으로 표현이 가능함

​

5. 회귀분석 결과 검증 - 잔차 확인 및 그래프 그리기

 

이러한 결과를 검증해보기 위해 기존 시트의 데이터를 하나 더 복사해서 확인해보도록 해보겠습니다.

 

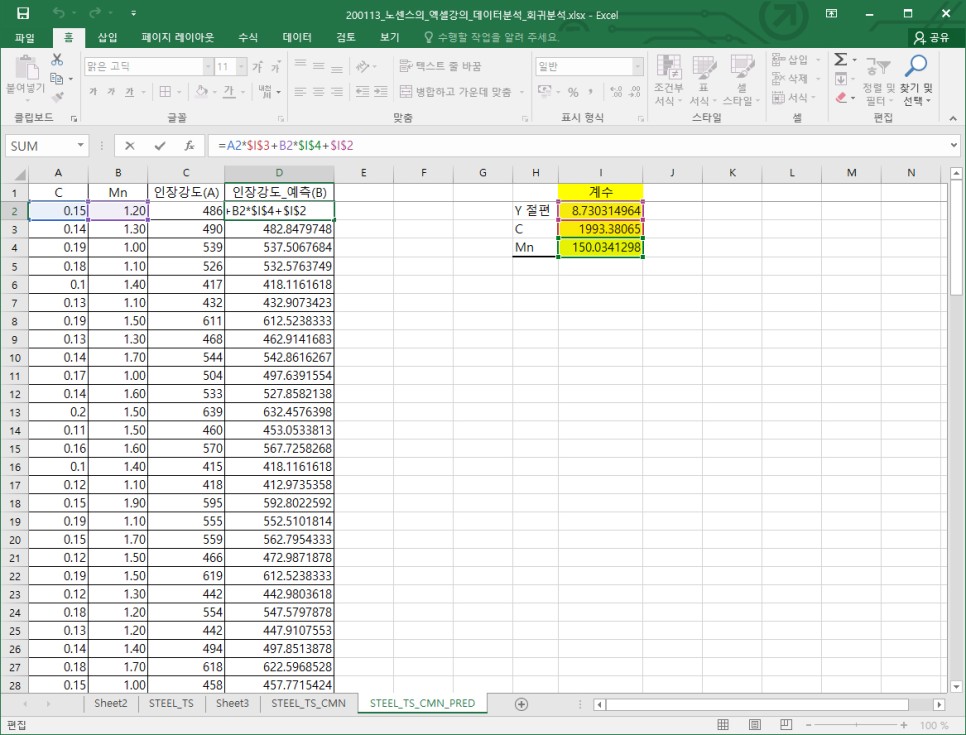
시트 이름은 "STEEL_TS_CMN_PRED"라고 만들고, 2번째 회귀분석에서 계수 부분값을 복사해서 빈 공간에 붙여넣은 뒤 "D"열에 "인장강도_예측(B)"라는 열을 하나 만듭니다. 이후에 "D2"에 회귀계수와 절편을 이용해 인장강도를 예상할 수 있게 계산식을 작성합니다. 그리고 "E"열에 "잔차(B-A)"라는 열을 하나 더 만들고 인장강도 예측값이 "D"열에서 인장강도 실측값인 "C"열을 빼 잔차를 구해 봅니다. 그러면 대략적으로 실측값과 예측값이 얼마나 차이가 있는지를 알 수 있습니다.

 

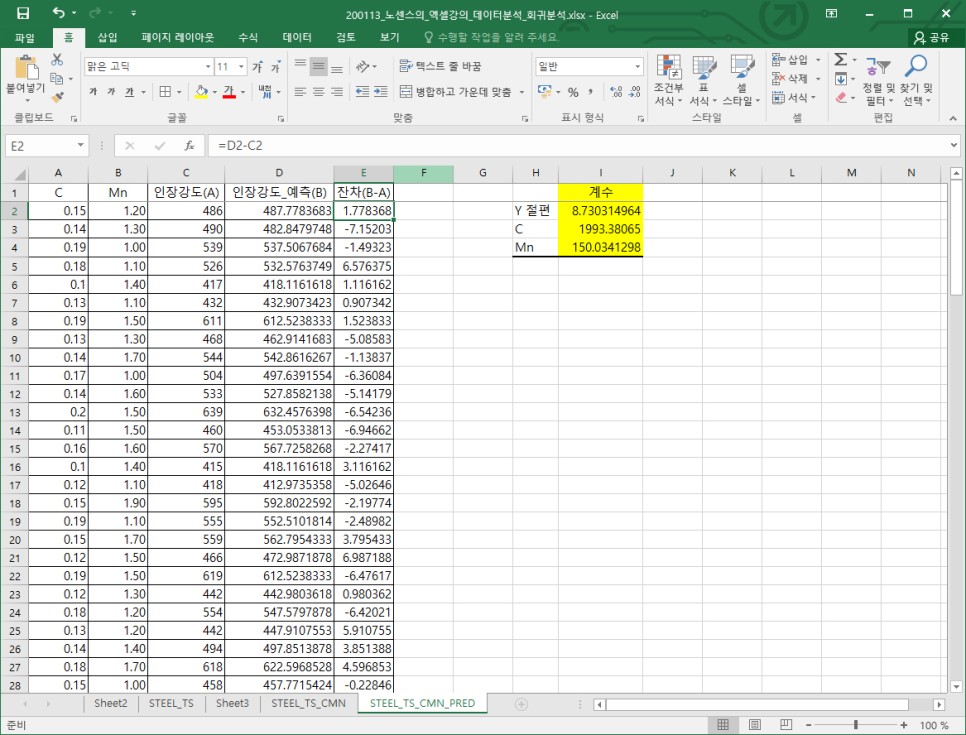
이러한 결과를 보다 쉽게 파악하기 위해 그래프를 그려서 실측값과 예측값을 비교해 보도록 하겠습니다. "C"와 "D"열을 선택한 뒤 삽입 메뉴에서 "표식이 있는 꺾은선형" 그래프를 선택합니다.

 

그리고 세로 축을 선택한 후 마우스 우측 클릭을 통해 "축 서식"에 들어가 축 옵션에서 최소값을 300, 최대값을 700으로 변경해줍니다.

 

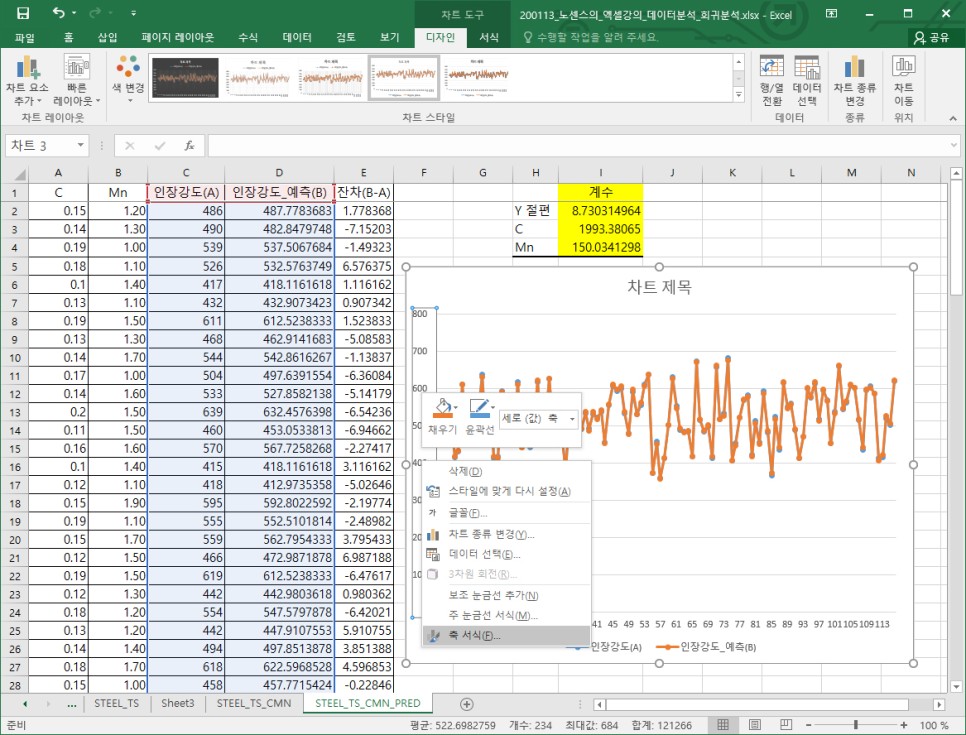
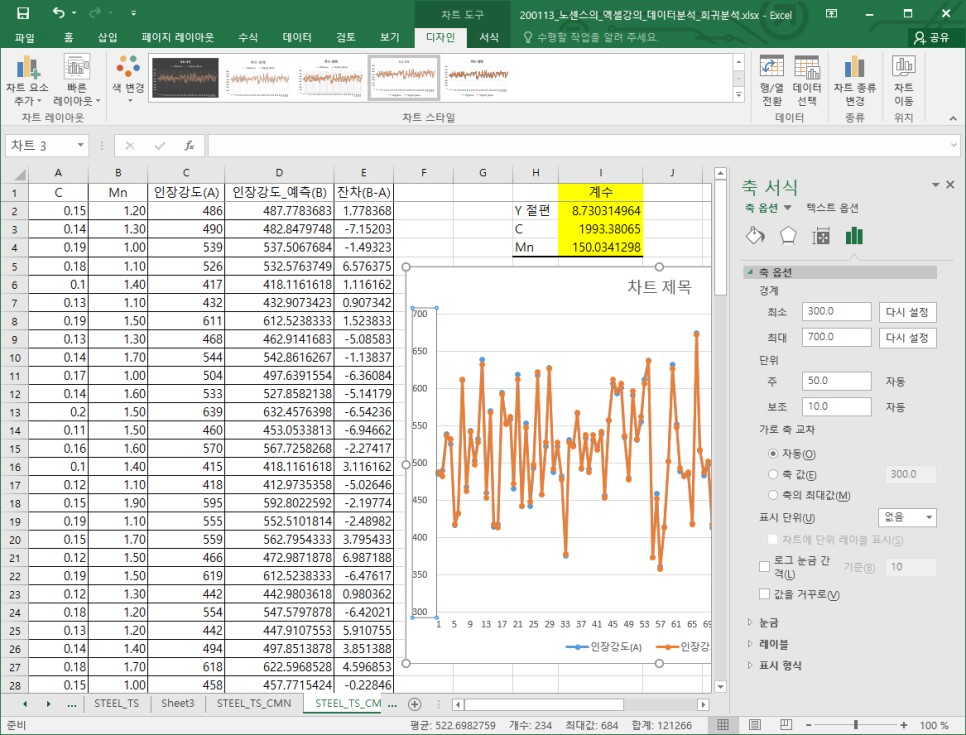
그러면 아래와 같이 실측값과 예측값을 1:1로 비교해 볼 수 있는 꺾은 선 그래프를 그려볼 수 있습니다. 꺾은 선을 통해 실측값과 예측값이 거의 유사함을 알 수 있습니다.

 

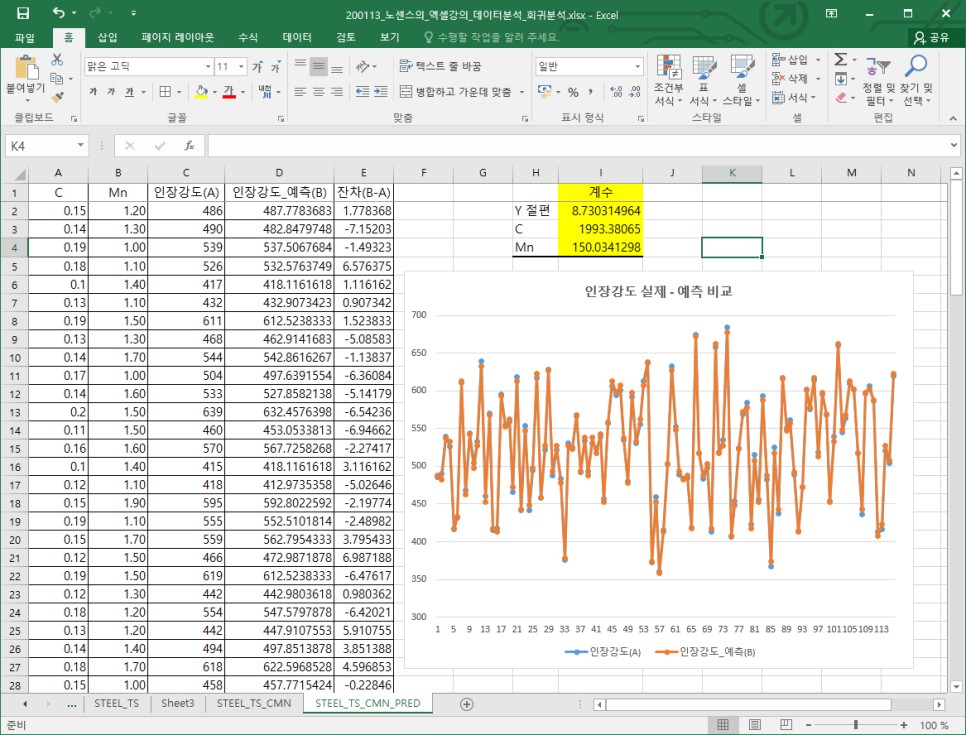
상기 사례의 경우 임의로 생성한 데이터로 수행한 회귀분석이기 때문에 매우 높은 결정계수가 도출되었지만 실제 업무를 수행하다보면 0.5를 넘기도 어려운 경우가 부지기수입니다. 이러한 때에 다양한 경험과 지식, 노하우를 통해 결정계수를 향상시킬 수 있습니다. 회귀분석은 주로 선형관계를 예측할 때 적합하며 독립변수와 종속변수가 1:1일 경우엔 자연로그(ln)나 지수, 제곱 등의 형태로 비선형관계를 예측할 수도 있습니다. 더 상세한 부분들은 차후 R을 이용한 회귀분석에서 다루도록 하겠습니다.

​

읽어주셔서 감사합니다.

 

※ 문의사항은 댓글 남겨주시고, 도움이 되셨다면 공감 버튼 부탁드리겠습니다. ^-^

 

200113_노센스의_엑셀강의_데이터분석_회귀분석.xlsx

0.04MB